bir sözlükte eksik olmaması gereken başlıklardan biri. bu başlık altında laik sözlük yazarlarının ne gibi şeylerden dolayı ufuklarını ikiye katladıklarını okumak zevkli olacaktır diye tahmin diyorum.
öğrenildiğinde ufku iki katına çıkaran şeyler
Enerji maddeye donusebilir.
Edit: eşit değildir
Edit: eşit değildir
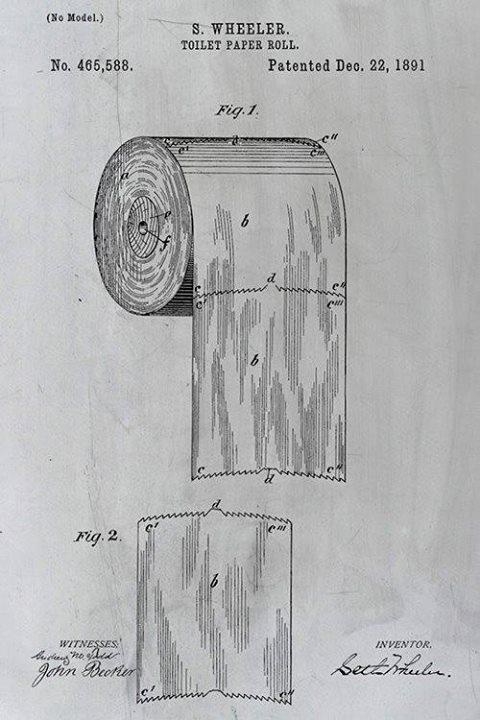
tuvalet kağıdının yaprakları üstten gelmelidir buyrun bu da 1891 tarihli patent belgesidir

ölüm korkusu durduk yere kafanızın içine girince sizi çökertebilen bişey aylarca bu korku ile nedensizce düşünüp ağladım ama ögrendiğimde farkettim ki geçirdiğimiz en s.ktiri boktn günün ne kadar kıymetli ve değerli olduğunu.
Babamın arabasını aldığımda benzin göstergesini full görmek
Dünyadaki çoğu bilgiyi canlıların ölmesiyle elde ettiğimiz gerçeği.
dünyadaki insanların %25'inin hayatında hiç kar görmemiş olması.
türkiye'nin %54'ünün et ürünleri yiyememesi. Aslında normal bir olay ama olsun paylaşayım.
1.Evrim (salt biyolojik değil kültür vs dahil)
(bkz:evrim sürüyor)
2.Sınıfların olduğu toplumların çelişkileri
(bkz:insanlık tarihi sınıf savaşımları tarihidir)
Bu ikisi tabiki yeterli gelmez ama bugünkü dünyaya, geçmişe ve geleceğe bakarken bu iki olgu üzerinden değerlendirebilmek ufkumu baya baya açtı.
(bkz:evrim sürüyor)
2.Sınıfların olduğu toplumların çelişkileri
(bkz:insanlık tarihi sınıf savaşımları tarihidir)
Bu ikisi tabiki yeterli gelmez ama bugünkü dünyaya, geçmişe ve geleceğe bakarken bu iki olgu üzerinden değerlendirebilmek ufkumu baya baya açtı.
insana aydınlanma yaşatan olaylardır. bunlardan biri de Tüm tavukların yumurtadan çıkmış olmasıdır. "Sorunun cevabını basitçe anlayabilmek için, sözde paradoksun aktörleri olan "tavuk" ve "yumurta"yı tanımamız gerekir. Tavuk ile başlayalım: Bugün net bir şekilde bildiğimiz üzere tüm kuşlar, 240 milyon yıl kadar önce dinozorlardan ayrılarak evrimleşmiştir. Tavuk, bir kuş türüdür, dolayısıyla kökenleri dinozorlara kadar takip edilebilir. Bilindiği üzere tüm kuşlar yumurtlayarak ürerler. Bu sebeple, şimdi de yumurtanın tarihine kısaca bakalım: yumurta dediğimiz kabuklu, karalarda bırakıldığında içerisindeki embriyoyu koruyup besleyebilecek özellikteki üreme yapısının ilk örneklerine 340 milyon yıl kadar önce amfibilerde ve onlardan evrimleşen sürüngenlerde rastlıyoruz.
Evrim tarihini takip edecek olursak, balıklardan evrimleşen amfibiler ilk büyük yumurtaları nemli kumsallara bırakmaya başlamışlardır. Daha sonradan amfibilerden evrimleşen sürüngenler yumurtlayarak üremeyi sürdürmüşlerdir ve bir adım öteye götürerek amniyotik kese sayesinde nemli olmayan, kurak kara parçalarında da üreyebilmeye başlamışlardır. Sürüngenlerin bir kolu dinozorlara evrimleşmiş, bu koldan ayrılan bir grup da kuşlara ve nihayetinde tavuklara evrimleşmiştir. Dolayısıyla bu soy hattı boyunca her canlı bir yumurtadan çıkmıştır. Tam olarak bu sebeple, ilkin tavuklar da dahil olmak üzere tüm tavuklar da öyle... Bu da, sorumuzun cevabını tartışmasız bir şekilde vermektedir: yumurta, tavuktan önce evrimleşmiştir, dolayısıyla tavuk yumurtadan çıkar.
Sorunun daha derin olarak sorduğuysa "Yumurtalayarak üreyen bir hayvanın yumurtası mı, kendisi mi önce evrimleşmiştir?" sorusudur. Yumurtanın evrimini daha sonraki bir makalemizde detaylı olarak işleyeceğiz; ancak paradoks biçiminde sunulan bu soru, evrimin kademeli doğasını anlayamamaktan kaynaklanmaktadır. Çünkü sorunun bir diğer formu olan ve aslen sorduğu şeyi özetleyen soru şudur: "Bir canlının ebeveyni de, çocuğu da kendisi ile aynı türken, evrim nasıl yeni türler yaratır?" Bu soruyu aynı başlıklı şu makalemizde işlemiştik: hiçbir zaman tek bir nesilde yeni bir tür var olmaz, bu süreç kademelidir. Dolayısıyla asla bir yumurta bir anda evrimleşiverip, ondan da yeni bir kuş türü oluşmamıştır. Zaten buna gerek de yoktur. Yumurta ile o yumurtanın barındıracağı tür bir arada evrimleşir. Her evrimsel nesil içerisinde yumurta o türün özelliklerini daha fazla barındırır hale gelirken, o yumurtalardan çıkan bireyler de yeni bir türün özelliklerini daha çok barındırır hale gelir. Yani bir tavuğun var olması için "tavuk yumurtası" gerekmez, çünkü tavuk tek bir nesilde evrimleşmiş bir canlı türü değildir. Tıpkı köpeklerin Yapay Seçilim sonucu kurtlardan evrimleşirken hiçbir zaman tek bir nesilde bir Çivava'nın ya da bir Danua'nın ortaya çıkmaması gibi; ancak her nesilde o çeşidin özelliklerini daha fazla taşıyan bireylerin ortaya çıkması ve seçilmesi gibi...
Ne olursa olsun, her tavuk yumurtadan çıkmıştır. Dolayısıyla yumurta önce gelmiştir.
* "Yumurtadan çıkan tavuk değil, civcivdir." diye düşünen okurlarımız için: Tavuk sadece bu yazının konusu olan kuşun dişilerinin ismi değildir, aynı zaman Gallus gallus domesticus alt türünün Türkçedeki adıdır. Yazıda da bu şekilde kullanılmıştır. Tavuk ve horoz ayrı türler değildir; genellikle "tavuk" olarak bildiğimiz hayvanın dişisi ile erkeğinin isimleridir."
-alıntı-
ilgili yazı: http://www.evrimagaci.org/soru-cevap/44
hena'ya selamlar.
Evrim tarihini takip edecek olursak, balıklardan evrimleşen amfibiler ilk büyük yumurtaları nemli kumsallara bırakmaya başlamışlardır. Daha sonradan amfibilerden evrimleşen sürüngenler yumurtlayarak üremeyi sürdürmüşlerdir ve bir adım öteye götürerek amniyotik kese sayesinde nemli olmayan, kurak kara parçalarında da üreyebilmeye başlamışlardır. Sürüngenlerin bir kolu dinozorlara evrimleşmiş, bu koldan ayrılan bir grup da kuşlara ve nihayetinde tavuklara evrimleşmiştir. Dolayısıyla bu soy hattı boyunca her canlı bir yumurtadan çıkmıştır. Tam olarak bu sebeple, ilkin tavuklar da dahil olmak üzere tüm tavuklar da öyle... Bu da, sorumuzun cevabını tartışmasız bir şekilde vermektedir: yumurta, tavuktan önce evrimleşmiştir, dolayısıyla tavuk yumurtadan çıkar.
Sorunun daha derin olarak sorduğuysa "Yumurtalayarak üreyen bir hayvanın yumurtası mı, kendisi mi önce evrimleşmiştir?" sorusudur. Yumurtanın evrimini daha sonraki bir makalemizde detaylı olarak işleyeceğiz; ancak paradoks biçiminde sunulan bu soru, evrimin kademeli doğasını anlayamamaktan kaynaklanmaktadır. Çünkü sorunun bir diğer formu olan ve aslen sorduğu şeyi özetleyen soru şudur: "Bir canlının ebeveyni de, çocuğu da kendisi ile aynı türken, evrim nasıl yeni türler yaratır?" Bu soruyu aynı başlıklı şu makalemizde işlemiştik: hiçbir zaman tek bir nesilde yeni bir tür var olmaz, bu süreç kademelidir. Dolayısıyla asla bir yumurta bir anda evrimleşiverip, ondan da yeni bir kuş türü oluşmamıştır. Zaten buna gerek de yoktur. Yumurta ile o yumurtanın barındıracağı tür bir arada evrimleşir. Her evrimsel nesil içerisinde yumurta o türün özelliklerini daha fazla barındırır hale gelirken, o yumurtalardan çıkan bireyler de yeni bir türün özelliklerini daha çok barındırır hale gelir. Yani bir tavuğun var olması için "tavuk yumurtası" gerekmez, çünkü tavuk tek bir nesilde evrimleşmiş bir canlı türü değildir. Tıpkı köpeklerin Yapay Seçilim sonucu kurtlardan evrimleşirken hiçbir zaman tek bir nesilde bir Çivava'nın ya da bir Danua'nın ortaya çıkmaması gibi; ancak her nesilde o çeşidin özelliklerini daha fazla taşıyan bireylerin ortaya çıkması ve seçilmesi gibi...
Ne olursa olsun, her tavuk yumurtadan çıkmıştır. Dolayısıyla yumurta önce gelmiştir.
* "Yumurtadan çıkan tavuk değil, civcivdir." diye düşünen okurlarımız için: Tavuk sadece bu yazının konusu olan kuşun dişilerinin ismi değildir, aynı zaman Gallus gallus domesticus alt türünün Türkçedeki adıdır. Yazıda da bu şekilde kullanılmıştır. Tavuk ve horoz ayrı türler değildir; genellikle "tavuk" olarak bildiğimiz hayvanın dişisi ile erkeğinin isimleridir."
-alıntı-
ilgili yazı: http://www.evrimagaci.org/soru-cevap/44
hena'ya selamlar.
1- Güneş merkezli dünya modeli: yanlış hatırlamıyor isem Kopernik tarafından ispat edilmiş idi. Bu öğrenilene dek dünya sabit, güneş dahil diğer gezegen ve yıldızlar onun etrafında dönüyor zannediliyordu. Şimdi biliyoruz ki güneş sabit, dünya ve diğer gezegenler onun etrafında dönmekte. Ama güneşte samanyolu galaksisinde sabit değil, turlar atmaktadır. Tabii onun sayesinde bizde.
2- evrende dokunulabilecek kadar soğuk yıldızların olması: bütün yıldızlar güneş gibi aşırı sıcak değildir. Evren insan eliyle dokunulabilecek kadar soğuk yıldızlar ile doludur. bu yıldızlar ya yeni doğmuş ya dada süpernovadan önce ölmek üzere idi.
Bu giriyi şu bilgilerden emin olduktan sonra editleyeceğim.
Edit;
1- Kendisinden çok önce Aristarchus ve ondan birkaç yüzyıl sonra Biruni (ve aradaki birçok kişi) kopernik'e atfedilen güneş merkezli “dünya” modelini dile getirmiş. Fakat Copernicus'u onlardan ayıran, onun gözlemlerini, savını destekleyecek biçimde bir yayın haline getirmesiymiş. Güneş merkezli evren modeline ulaşmak için yaptığı gözlemleri, “başkalarının da tekrarlayabileceği” biçimde toplamış, delillerini ortaya koymuş. Tıpkı, mikrobun (tek hücreli canlıların) varlığını eski Yunan düşünürlerinin ve bizden Akşemseddin'in dile getirmesi gibi. Fakat, mikrobun varlığını ve nasıl bir şey olduğunu şüpheye yer bırakmayacak biçimde açıklayan Pasteur'dur.
2- ölmek üzere olan yıldızlar imiş. Bunun hakkında daha detaylı bilgi için kahverengi ve kara cüceleri araştırabilirsiniz.
2- evrende dokunulabilecek kadar soğuk yıldızların olması: bütün yıldızlar güneş gibi aşırı sıcak değildir. Evren insan eliyle dokunulabilecek kadar soğuk yıldızlar ile doludur. bu yıldızlar ya yeni doğmuş ya dada süpernovadan önce ölmek üzere idi.
Bu giriyi şu bilgilerden emin olduktan sonra editleyeceğim.
Edit;
1- Kendisinden çok önce Aristarchus ve ondan birkaç yüzyıl sonra Biruni (ve aradaki birçok kişi) kopernik'e atfedilen güneş merkezli “dünya” modelini dile getirmiş. Fakat Copernicus'u onlardan ayıran, onun gözlemlerini, savını destekleyecek biçimde bir yayın haline getirmesiymiş. Güneş merkezli evren modeline ulaşmak için yaptığı gözlemleri, “başkalarının da tekrarlayabileceği” biçimde toplamış, delillerini ortaya koymuş. Tıpkı, mikrobun (tek hücreli canlıların) varlığını eski Yunan düşünürlerinin ve bizden Akşemseddin'in dile getirmesi gibi. Fakat, mikrobun varlığını ve nasıl bir şey olduğunu şüpheye yer bırakmayacak biçimde açıklayan Pasteur'dur.
2- ölmek üzere olan yıldızlar imiş. Bunun hakkında daha detaylı bilgi için kahverengi ve kara cüceleri araştırabilirsiniz.
Tavukların atasının dinozorlar olması çok trajikomik değil mi? senin atan dünyanın en büyük ve güçlü canlılarından olsun, herkes ondan korksun, sen ayranla 3 liraya satıl. olacak şey değil. türkler de öyle. ondan sonra yunanlar da böyle. aristo'dan sonra borcunu rüşvetle gizleyip batan ülkeye dönüştüler.
bildiğiniz tüm sayılar aslında argand düzlemi üzerinde yer alır.
ım(z)=0 alınırsa argand düzleminde bilinen her sayı türü için yer vardır. bu şekilde düşünülünce yazılabilecek tüm karmaşık sayılar diğer sayı türlerinden çok daha fazladır.
şimdi bu çok, nasıl çok, ne kadar çok?
karmaşık sayılar dışarıda tutularak bilinen en "geniş" küme gerçel sayılar kümesi olsun. sayı doğrusu üzerinde gösterilebilinir, değil mi? hatta buna x- ekseni diyelim, 0'dan geçmek suretiyle x-eksenine dik olacak şekilde bir y-ekseni konduralım, kabaca argand diyagramı'nı elde ettik.
-koordinat düzlemi ulan bu işte? argand da ne oluyor varg yeme bizi, derseniz haklısınız. fakat teşbihte hata olmaz. argand düzlemi klasik koordinat sistemi için x yerine re, y yerine de im yazılmasıyla oluşturulur bunu noktanın birimi olarak düşünebilirsiniz aslında.-
bizim karmaşık sayılar dediğimiz sayılar bu düzlemin herhangi bir noktasına denk gelir.
yeri gelmişken biraz analizini yapalım bu efsane sayıların.
z = a + bi, standart z karmaşık sayısının gösterilişidir. burada a, re(z) = a gerçel kısımdır yukarıda bahsettiğim "gerçel" sayılardan biridir. im(z) = b de öyle, imajiner doğru üzerinde "gerçel" bir sayıdır gerçel olmasına fakat b, z karmaşık sayısındaki i'nin kat sayısıdır.
argand düzleminde bir z sayısını bileşenlerince resmetmek mümkündür; re ekseni üzerindeki a sayısı, im ekseni üzerindeki b sayısı ile (a,b) noktası elde edilir ve bu nokta sıfır noktası ile birleştirilir. elde edilen "konum vektörü" z sayısıdır.
tam da burada, *ne aşina bir arkadaş diyebilir ki, hop! ben bunu bir t açsı ve bir r uzaklığı kullanarak ifade etmek istiyorum. hay hay, ifade edelim.
burada t açısına, karmaşık sayının argümanı r uzaklığına da karmaşık sayının modülü diyeceğiz.
uzaklık dedik, değil mi? e, kutupsal koordinat sistemine de aşinayız. iki nokta arasındaki uzaklığı nasıl buluyoruz? ((x1-x2)^2+(y1-y2)^2)^(1/2) şeklinde değil mi? bunu karmaşık sayının modülü için düzenlersek, unutmamamız gereken olay, karmaşık sayıların bir ayağının hep 0+0i'de olduğudur. yani başlangıç noktasında.
r = |z| = (a^2 + b^2)^(1/2)
şeklinde modülü tayin ederiz. t argümanı peki?
a,b ve r dikkatli incelendiğinde bir dik üçgen üretmezler mi argand düzlemi üzerinde? eski dostum trigonometri! t argümanı notasyonumuz gereğince, a ile r arasında değil midir?
tant = b/a => ? = tan^-1(b/a) ile bulunur.
ee iyi de, ya bunlar t ve r verir de sayıyı isterse napacağız, bulabilir miyiz?
tabii ki de.
ne dedik yukarıda? açı var ve dik üçgen var e öyleyse oradan hareketle, cost = a/r yazmak mümkündür. her iki tarafı r ile çarpıp ifadeyi daha temiz yazabiliyorken, yazalım.
rcost = a
ve
rsint = b elde edilir.
güzel de, bunu nasıl yazacağız?
z = r.cost + r.sint.i euler formülüne aşina mıyız?
-tam burada euler formüllerinden bahsetmek istiyorum belki ayrı bir başlık altında da yazılabilirdi fakat böyle yapacağım.
e üzeri x'in maclaurin serisini de mi anlatsam, o zaman sin(x)'in ve cos(x)'in maclaurin serilerini de açmam lazım. onları açmayıp kullanacağım.
p(cos(x)) = 1 - x^2/2! + x^4/4! - ... (çift terimler)
p(sin(x)) = x - x^3/3! + x^5/5! - ... (tek terimler)
neden f(x) = e^x? e'yi bu kadar önemli kılan ne? elbette e^x'in türevinin de e^x olması.
f(x) = e^x = f'(x) = f''(x) = ... = f(n)(x) = ... yani türevi alındıkça eğri üzerinde her noktadaki eğim o noktadaki fonksiyon değerine eşit!
bu kadar e hayranlığı yeter bence, e'nin maclaurin serisi'ni ifade etmeye çalışalım biraz.
maclaurin serisi, taylor serisi'nin sıfır merkezlisidir. seriyi ve açılışını çıkartmayacağım fakat kullanıyorum yine. *
e^0 = 1 = f(0) = f'(0) = ...
e^x = 1 + x^1/1! + x^2/2! + x^3/3! ...
burada e'nin kendisini bulmak, x = 1 için sonuç verecektir. -en azından yaklaşılır-
bu yazılım, sin(x) ve cos(x)'in maclaurin serisini andırıyor fakat işaretleri tutmuyor.
x yerine, ix alsak? normalde bu çok saçma olurdu fakat sonsuz tane terim ve polinom açılımı için konuşuyoruz. (i^2 = -1, i^3 = -i, i^4 = 1) ne de olsa.
polinomda x gördüğümüz yere ix yazıp düzenlersek,
f(ix) = e^(ix) = 1 + ix - x^2/2! -i.x^3/3! + x^4/4! + i.x^5/5! - ... bazı terimer gerçel bazıları sanal ilerliyor. gerçel ve sanal terimleri ayırıp yazalım.
re(e^(ix)) = 1 - x^2/2! + x^4/4! - x^6/6! + ...
im(e^(ix)) = x - x^3/3! + x^5/5! - x^7/7! + ...
ee? gerçel kısım, re(e^(ix)) = p(cos(x)) oldu! yani cos(x)'in maclaurin serisine sanal kısım da sin(x)'in maclaurin serisine eşit çıktı. sonuç olarak,
e^(ix) = cosx + i.sinx (euler formülü)
formülü bir adım öteye taşımak da mümkün. radyan kullanalım ve x'i pi'ye eşitleyelim.
e^(i.pi) = -1 ki bu da euler özdeşliği olarak ifade edilir. hatta klasik yazalım;
e^(i.pi) + 1 = 0
bu özdeşlik, beni acayip mutlu ediyor. bunun ne olduğunu bilmek aslında birbirlerinden epey uzakta, farklı zamanlarda yaşamış insanlarca keşfedilen bu sembollerin kusursuz bir özdeşlik haline gelmesi ve tüm bu süreci anlayabiliyor olmak... ayy ağlıcam galiba.-
bir adım daha gitsek r parantezine alsak ifadeyi?
z = r(cost + i.sint) bu ifadeyi, euler formülünden yararlanarak yazabiliriz şöyle ki;
z = r.e^(it)
(bkz:hiperbolik sayılar)
(bkz:dördeyler)
(bkz:yüksek-boyutlu gama matrisler)
(bkz:dalga fonksiyonu)
[bkz][clifford cebiri/bkz]
ım(z)=0 alınırsa argand düzleminde bilinen her sayı türü için yer vardır. bu şekilde düşünülünce yazılabilecek tüm karmaşık sayılar diğer sayı türlerinden çok daha fazladır.
şimdi bu çok, nasıl çok, ne kadar çok?
karmaşık sayılar dışarıda tutularak bilinen en "geniş" küme gerçel sayılar kümesi olsun. sayı doğrusu üzerinde gösterilebilinir, değil mi? hatta buna x- ekseni diyelim, 0'dan geçmek suretiyle x-eksenine dik olacak şekilde bir y-ekseni konduralım, kabaca argand diyagramı'nı elde ettik.
-koordinat düzlemi ulan bu işte? argand da ne oluyor varg yeme bizi, derseniz haklısınız. fakat teşbihte hata olmaz. argand düzlemi klasik koordinat sistemi için x yerine re, y yerine de im yazılmasıyla oluşturulur bunu noktanın birimi olarak düşünebilirsiniz aslında.-
bizim karmaşık sayılar dediğimiz sayılar bu düzlemin herhangi bir noktasına denk gelir.
yeri gelmişken biraz analizini yapalım bu efsane sayıların.
z = a + bi, standart z karmaşık sayısının gösterilişidir. burada a, re(z) = a gerçel kısımdır yukarıda bahsettiğim "gerçel" sayılardan biridir. im(z) = b de öyle, imajiner doğru üzerinde "gerçel" bir sayıdır gerçel olmasına fakat b, z karmaşık sayısındaki i'nin kat sayısıdır.
argand düzleminde bir z sayısını bileşenlerince resmetmek mümkündür; re ekseni üzerindeki a sayısı, im ekseni üzerindeki b sayısı ile (a,b) noktası elde edilir ve bu nokta sıfır noktası ile birleştirilir. elde edilen "konum vektörü" z sayısıdır.
tam da burada, *ne aşina bir arkadaş diyebilir ki, hop! ben bunu bir t açsı ve bir r uzaklığı kullanarak ifade etmek istiyorum. hay hay, ifade edelim.
burada t açısına, karmaşık sayının argümanı r uzaklığına da karmaşık sayının modülü diyeceğiz.
uzaklık dedik, değil mi? e, kutupsal koordinat sistemine de aşinayız. iki nokta arasındaki uzaklığı nasıl buluyoruz? ((x1-x2)^2+(y1-y2)^2)^(1/2) şeklinde değil mi? bunu karmaşık sayının modülü için düzenlersek, unutmamamız gereken olay, karmaşık sayıların bir ayağının hep 0+0i'de olduğudur. yani başlangıç noktasında.
r = |z| = (a^2 + b^2)^(1/2)
şeklinde modülü tayin ederiz. t argümanı peki?
a,b ve r dikkatli incelendiğinde bir dik üçgen üretmezler mi argand düzlemi üzerinde? eski dostum trigonometri! t argümanı notasyonumuz gereğince, a ile r arasında değil midir?
tant = b/a => ? = tan^-1(b/a) ile bulunur.
ee iyi de, ya bunlar t ve r verir de sayıyı isterse napacağız, bulabilir miyiz?
tabii ki de.
ne dedik yukarıda? açı var ve dik üçgen var e öyleyse oradan hareketle, cost = a/r yazmak mümkündür. her iki tarafı r ile çarpıp ifadeyi daha temiz yazabiliyorken, yazalım.
rcost = a
ve
rsint = b elde edilir.
güzel de, bunu nasıl yazacağız?
z = r.cost + r.sint.i euler formülüne aşina mıyız?
-tam burada euler formüllerinden bahsetmek istiyorum belki ayrı bir başlık altında da yazılabilirdi fakat böyle yapacağım.
e üzeri x'in maclaurin serisini de mi anlatsam, o zaman sin(x)'in ve cos(x)'in maclaurin serilerini de açmam lazım. onları açmayıp kullanacağım.
p(cos(x)) = 1 - x^2/2! + x^4/4! - ... (çift terimler)
p(sin(x)) = x - x^3/3! + x^5/5! - ... (tek terimler)
neden f(x) = e^x? e'yi bu kadar önemli kılan ne? elbette e^x'in türevinin de e^x olması.
f(x) = e^x = f'(x) = f''(x) = ... = f(n)(x) = ... yani türevi alındıkça eğri üzerinde her noktadaki eğim o noktadaki fonksiyon değerine eşit!
bu kadar e hayranlığı yeter bence, e'nin maclaurin serisi'ni ifade etmeye çalışalım biraz.
maclaurin serisi, taylor serisi'nin sıfır merkezlisidir. seriyi ve açılışını çıkartmayacağım fakat kullanıyorum yine. *
e^0 = 1 = f(0) = f'(0) = ...
e^x = 1 + x^1/1! + x^2/2! + x^3/3! ...
burada e'nin kendisini bulmak, x = 1 için sonuç verecektir. -en azından yaklaşılır-
bu yazılım, sin(x) ve cos(x)'in maclaurin serisini andırıyor fakat işaretleri tutmuyor.
x yerine, ix alsak? normalde bu çok saçma olurdu fakat sonsuz tane terim ve polinom açılımı için konuşuyoruz. (i^2 = -1, i^3 = -i, i^4 = 1) ne de olsa.
polinomda x gördüğümüz yere ix yazıp düzenlersek,
f(ix) = e^(ix) = 1 + ix - x^2/2! -i.x^3/3! + x^4/4! + i.x^5/5! - ... bazı terimer gerçel bazıları sanal ilerliyor. gerçel ve sanal terimleri ayırıp yazalım.
re(e^(ix)) = 1 - x^2/2! + x^4/4! - x^6/6! + ...
im(e^(ix)) = x - x^3/3! + x^5/5! - x^7/7! + ...
ee? gerçel kısım, re(e^(ix)) = p(cos(x)) oldu! yani cos(x)'in maclaurin serisine sanal kısım da sin(x)'in maclaurin serisine eşit çıktı. sonuç olarak,
e^(ix) = cosx + i.sinx (euler formülü)
formülü bir adım öteye taşımak da mümkün. radyan kullanalım ve x'i pi'ye eşitleyelim.
e^(i.pi) = -1 ki bu da euler özdeşliği olarak ifade edilir. hatta klasik yazalım;
e^(i.pi) + 1 = 0
bu özdeşlik, beni acayip mutlu ediyor. bunun ne olduğunu bilmek aslında birbirlerinden epey uzakta, farklı zamanlarda yaşamış insanlarca keşfedilen bu sembollerin kusursuz bir özdeşlik haline gelmesi ve tüm bu süreci anlayabiliyor olmak... ayy ağlıcam galiba.-
bir adım daha gitsek r parantezine alsak ifadeyi?
z = r(cost + i.sint) bu ifadeyi, euler formülünden yararlanarak yazabiliriz şöyle ki;
z = r.e^(it)
(bkz:hiperbolik sayılar)
(bkz:dördeyler)
(bkz:yüksek-boyutlu gama matrisler)
(bkz:dalga fonksiyonu)
[bkz][clifford cebiri/bkz]
basit hesap makineleriyle üslü sayı hesaplamak;
üslü sayının tabanını yazıp bir kere çarpıya bastıktan sonra kuvvetin bir eksiği kadar eşittire basılır.
örnek: 4 üzeri 3 için; 4, çarpı, eşittir,eşittir tuşlayarak sonuca ulaşılabilir.
Sonradan ekleme:
manfred von richthofen adlı alman savaş pilotunun birinci dünya savaşı'nda tam 80 tane düşman uçak düşürmesi. kırmızıya boyadığı uçağını gören bazı düşman pilotlarının onu görünce kaçmaları, karşılaştığı uçağı önce düelloya davet etmesi nedeniyle düşmanları tarafından kendisine saygı duyulması, uçağı düşürülüp hayatını kaybettikten sonra savaşta almanya'nın düşmanı olan fransa tarafından eksiksiz bir askeri törenle gömülmesi. ve bütün bunları yapıp hayatını kaybettiğinde sadece 26 yaşındaydı
üslü sayının tabanını yazıp bir kere çarpıya bastıktan sonra kuvvetin bir eksiği kadar eşittire basılır.
örnek: 4 üzeri 3 için; 4, çarpı, eşittir,eşittir tuşlayarak sonuca ulaşılabilir.
Sonradan ekleme:
manfred von richthofen adlı alman savaş pilotunun birinci dünya savaşı'nda tam 80 tane düşman uçak düşürmesi. kırmızıya boyadığı uçağını gören bazı düşman pilotlarının onu görünce kaçmaları, karşılaştığı uçağı önce düelloya davet etmesi nedeniyle düşmanları tarafından kendisine saygı duyulması, uçağı düşürülüp hayatını kaybettikten sonra savaşta almanya'nın düşmanı olan fransa tarafından eksiksiz bir askeri törenle gömülmesi. ve bütün bunları yapıp hayatını kaybettiğinde sadece 26 yaşındaydı
Gerçek Daltonlar 1892 yılında giriştikleri başarısız bir banka soygununda öldürüldüler.

